Recently I read a New Yorker article about Brian Greene’s multimedia project, which paid tribute to some of Albert Einstein’s discoveries. It was launched on the centennial celebration of his general theory of relativity. Brian Greene is one of the more famous string theorists due to the popularity of his books which have included Fabric of the Cosmos and The Elegant Universe among others. He is a brilliant physicist and mathematician. In the article the author relates a story about Greene being set to the task of figuring out how many inches it is from here to the Andromeda galaxy by his father… when he was five. Not typical five-year-old work. Which then segues into a “consolation” for mathphobics that even Greene struggles to comprehend the homework assigned to his children in third and fifth grade.
“It’s all about strategies—‘Come up with a strategy’— and my kids are, like, ‘I don’t have a strategy, I just know it.’” Really? He has time for infinity, but can’t seem to piece together strategies for how students can learn to work with numbers?
We don’t “just know” things. If we know them, we know them for a reason – we understand something about how the numbers go together. It is simply a matter of slowing down and saying “How do I know that?” This is unsubtle Common Core and/or “new math” bashing, and it drives me crazy. For one thing, the article begins with a love letter to Albert Einstein who was able to put ideas together in new ways – to see hidden relationships – to manipulate ideas. This is how we (I’m a fifth grade teacher) teach kids to work with numbers! We use strategies, we take numbers apart to look at how they are constructed and put them back together in new ways. Consider the (5th grade) problem of 36 x 25. Where does sense-making occur?
| Standard Algorithm | Strategy: Doubling and Halving |
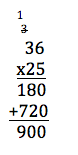 | 36 x 25 = 18 x 50 = 9 x 100 = 900 |
Mathematics is an art form. It is a dance that the human mind does with ideas within the science of pattern and order. The strategies we teach elementary students are well known to mathematicians.
To those who do not know mathematics, it is difficult to get across a real feeling as to the beauty, the deepest beauty, of nature…If you want to learn about nature, to appreciate nature, it is necessary to understand the language that she speaks in.
-Richard Feynman
And the brilliant and revered Feynman was even outdone (at least once!) in his “basic” understanding of arithmetic. An amusing story was related in James Gleick’s book Genius: The Life and Science of Richard Feynman, where the Nobel laureate Hans Bethe (one of Feynman’s mentors) out-computes Feynman with… you guessed it: a strategy.
When Bethe and Feynman went up against each other in games of calculating, they competed with special pleasure. Onlookers were often surprised, and not because the upstart Feynman bested his famous elder. On the contrary, more often the slow-speaking Bethe tended to out-compute Feynman. Early in the project they were working together on a formula that required the square of 48. Feynman reached across his desk for the Marchant mechanical calculator.
Bethe said, “It’s twenty-three hundred.”
Feynman started to punch the keys anyway. “You want to know exactly?” Bethe said. “It’s twenty-three hundred and four. Don’t you know how to take squares of numbers near fifty?” He explained the trick. Fifty squared is 2,500 (no thinking needed). For numbers a few more or less than 50, the approximate square is that many hundreds more or less than 2,500. Because 48 is 2 less than 50, 48 squared is 200 less than 2,500 — thus 2,300. To make a final tiny correction to the precise answer, just take that difference again — 2 — and square it. Thus 2,304.
(Feynman quote and anecdote found here)
Then to add insult to injury, Greene goes on to say that humans are not wired for math, but rather that we are wired to avoid lions or catch bison. I’m so confused. Is this the voice of someone who understands the language of mathematics to be both universal and unique to humans (in that we invented all of the math we have)? If the human mind is “wired,” it is certainly wired for math.
If ESSA is going to back off of on its support for the Common Core, that should not be an indictment of the principles and standards that have supported sense-making in mathematics. The math we teach students today helps them make sense of numbers the way that mathematicians make sense of numbers. The ideas are important, the strategies for working with numbers are important—the way students learn how to solve problems is important. We have no idea what the future holds for our ten-year-olds, but we know that they will need to be competent in understanding how to strategize, communicate, and reason. A Google search can tell you how far the Andromeda galaxy is from here. If that number is not in inches, a Google unit conversion will finish the job.
Let’s do some real math.
My motto for students like yours Dom and Jan is to have students engage in genuine problem solving opportunities and to focus on the Common Core Standards for Math Practice. I don’t ‘teach’ these standards to my students, but I ask them to engage this way. They consist of just what mathematicians do — look for patterns, persist, know whether or not things are making sense. Because I teach students in a social setting — school — the social element of having others understand their thinking is built in. Right now my sixth graders are in the midst of writing conjectures about what makes sense when dividing a fraction by a fraction. They have come up with three or more promising conjectures that are grounded in what it means to divide and the inherent division in every fraction. (One-half is one of something divided by two.) Their task will not be to get answers, but to convince each other that their conjecture works with all real numbers. So long as math is defined as answer-getting, as Brian Green seems to, then writing procedures for little kids can stand in for the kind of deep thinking and problem solving Brian Greene did as a five-year-old. My hope is for classrooms to meet the Brian Greens where they are not by saying ‘good enough’ when they get an answer, but instead asking them why it makes sense to them. Then learning to communicate does not have to be a gimmick but instead permeates their experience with mathematics.
Great article Spencer. This is one of the clearest explanations of how “new math” reflects actual mathematics practice rather than following a list of steps or algorithms. It’s the same fundamental idea as inquiry-based science education, to mimic the way knowledge is understood in the real world.
When I look at the problem 36×25, I can see that the answer is 900. I didn’t write down an algorithm, I would say that I just “knew” the answer. This is what I think you are seeing in some of your students Jan. But when I think about my mental process, I can see the way I got to that answer was by understanding how numbers relate to each other. I could see that 25 goes into 100 hundred 4 times and there are nine 4’s in 36. I “knew” the answer because I have a high comfort level with how numbers relate to each other. This is the same fundamentals of “new math”.
I see my High Cap students go through the same process. They can often solve problems like this so quickly that they don’t understand the process by which they did it. Your strategy Jan of having students explain how to do it to other students is exactly what these students need (as well as more challenging problems that make them slow down and think about how they can get to the solution). Student Generated Content for Learning where students teach other students their thought processes results in very high levels of student understanding and retention. This is what I was presenting on at the WAETAG conference Jan.
On the other hand, Spencer, if you ask highly intuitive thinkers (and individuals who test as highly gifted often also test as highly intuitive), “How did you get your answer?” or “What strategy did you use?” they will often answer “I don’t know” or “It just made sense.” They are not being contrary or defiant. They are being honest.
While most students follow steps from A to B to C to D in a logical process, intuitive thinkers go from A to Mars to the attic to “Oh, I get it.” Making them explain their reasoning would be as meaningless as asking them to explain how they manage to continue breathing while they run around at recess. And pushing them to explain their reasoning can make them frustrated or angry or even make them hate math.
I teach these kids math. Sometimes, when they don’t understand how to approach a problem, they ask me for help. I say, “If I were solving it, I would do this first.” I take ONE step out of the five or six or a dozen steps it would take me to figure out the solution. The intuitive thinker says, “Oh, now I get it.” Just from the first step.
So what do I do to prepare my intuitive thinkers for the CCSS tests? Because they have to know how to “show their thinking” in writing on the tests. I tell them to write directions for younger students to show them how to solve the problem. They may not be writing down the way they solved the problem, but they write down a legitimate way to solve the problem. And they write it down pretty thoroughly so the little kids will understand.
It’s a work-around. But the truth is, they don’t know how to explain their own thinking yet. They can’t translate Mars into English.
I am with you on this, Spencer. I was a good math student (probably a better math student than I was an English student), but it was because I was good at following directions, not because I understood what the math meant. That was why I was still utterly confused by credit card APRs in college. I took calculus, and over time and in non-classroom settings learned the strategies like the doubling and halving you illustrate above. I have such a keener understanding now of how numbers work than I did even when I finished calculus. It wasn’t until my second university calculus class (titled “Calculus for the Social Sciences”) when I finally realized that I was finding the area under the curve because that area actually gave me information, not just the computation.
My dad is a math teacher and so there may be genetic reasons all three of my sons are doing well with math… I think their success is in no small part because they have had teachers who understand that “common core math” isn’t different, it’s about understanding math. To date, I haven’t had the sense from any of my sons’ teachers that they are “afraid of this new math.” Understanding numbers, how they work, what they represent, and how to use them in different ways is useful…and actually isn’t new, as you indicate, it is what “good math thinkers” like Brian Greene figured out how to do earlier than the rest of us.
Pingback: Mathphilic on Stories from School https://t.co/x5… | EducatorAl's Tweets